The importance of size in reactor vessels
Some weeks ago, in this blog, we published a post called “Coffee Cup Calorimetry,” in which we explained this fascinating science from a day-to-day perspective. Today, we will discuss one of the critical concepts in calorimetry: the phi factor.
Imagine we have a normal coffee cup, not the polystyrene in the blog, as mentioned in an earlier post. It can probably contain 250 ml of delicious hot beverage to power us through the day. However, we know that it will not remain hot forever; instead, it will cool over time. The rate at which it cools down will depend on the volume the container retains and how much of the surface of the container is in contact with the surroundings.
One fascinating thing about heat exchange is the relationship between the rate at which the heat is transferred, the volume of the container, and the area. Let us imagine that we have a cylindrical tube, not too different from the coffee cup. If we increase the radius of the mug, doubling its size, the area of the mug will increase quadratically, whereas the volume increases in a cubic fashion. In plain terms, the volume will increase much faster than the area through which the heat can be exchanged.
But what does this mean for our cooling coffee? That means the bigger the mug, the slower it will cool down. For example, if our coffee were an espresso, cooling down by 1oC would not take more than 15 seconds. If we had it in a 1 L cafetiere, we would have to wait 2 minutes to achieve the same cooling. If we continue scaling up to an industrial scale, for example, a 25 m3 reactor, it would take 233 minutes. So now we can see how the radius, the area, and the volume affect cooling down.

What is the phi factor?
Phi factor is a correction factor based on the ratio of a vessel’s total heat capacity and the sample’s total heat capacity.
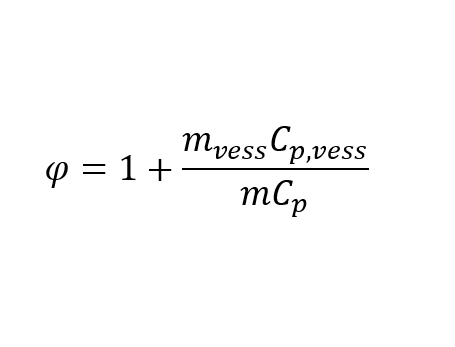
This coefficient indicates how much heat is required to heat up the vessel’s mass and content compared to the heat needed to heat the sample.
As we mentioned in the previous section, the vessel’s geometry and size will significantly impact the phi factor. For example, the larger the reactor, the smaller the surface will be in relation to the total volume. This, in turn, will mean that most of the energy will be used to heat the content instead of the reactor itself. As such, the phi factor will become progressively closer to 1, closer to adiabatic conditions.
Understanding this value is fundamental when planning adiabatic measurements because it is fundamental to understand not only the head lost to the environment but also the heat lost to the vessel, for example, a test cell. Understanding these parameters allows for the correction of the collected data.
For example, a phi factor of 1.2 means that the data acquired during the measurements needs to be adjusted ~20%, as 20% of the energy exchanged will be diverted towards heating the vessel. As a result, the closer the phi factor is to 1, the lower the influence of the container and the more representative the result is of the sample itself.
An essential factor to bear in mind is that chemical kinetics are nonlinear. Therefore, the values at particular high-phi factors can potentially overlook processes such as decomposition reactions.

Why do we care?
The phi factor helps us to correct values obtained by calorimetry. These values encompass thermodynamic values (enthalpy and equilibrium constants), kinetics values (reaction rates), and the characterization of material properties (phase transitions, melting points, specific heat capacities).
However, where calorimetry shines through and where phi factor corrections are fundamental is the design of safer processes. At a small scale, heat can be very easily and quickly dissipated to the surroundings. However, this process becomes critical at the industrial scale to avoid catastrophic events, such as decomposition reactions or thermal runaways. In large reactors, the sheer amount of reagent mass makes the reactor’s mass negligible, and following the equation means that the phi factor becomes 1. However, the phi factor can deviate substantially in normal size calorimeters used to simulate the conditions in those large reactors. Because of this, if a phi factor of 1 in the reactor cannot be achieved, at least it is of the utmost importance to understand what this value is for the test cells. Accurately quantifying the correction value contributes to trustworthy and reliable calorimetry data.
Conclusion
The Phi factor, expressed in such an easy, simple equation, has a profound impact in calorimetry, and it is fundamental for the calibration of the heat capacities of the vessels we use to measure energy exchanges. Acting as a correction factor, it ensures that the heat spent in heating up the container remains accounted for and, therefore, helps us to assess the chemical reactions we study accurately. This correction becomes particularly significant in safety and process engineering, helping to understand how to address potential thermal risks. So, as my coffee becomes cold after all that heat exchange, I want to draw your attention to the phi factor, the more-often-than-not-forgotten fighter in the pursuit of building a safer world.







